How
to check 3D congruence by comparing the shape of "elements-lines"
Regard a straight line from somewhere near the center
of the shell to the outline to mark out the place of an "element".
The isoline drawings on the following pages have been
completed with a number of such "elements". Equal numbers
show where equal "elements" where found on both "upper"
and "lower" parts of the arching.
To find out where equal "elements" are positioned
one has to start marking out the place for one of them by drawing
a straight line (marking out the place of the cross section to be
checked). The location of an other one has to be searched for. The
cross sectional shape of elements are equal when the distances between
a number of intersection points with the isolines following on each
other coincid with those already marked on the paper. Each isoline
represent a very special height on the surface of the shell. The arcshape
of an "element" that can be constructed is determined by
the location of the intersection points of "the element line"
with the "isolines".
This congruence can be checked in the following way:
1. Hold a piece of paper close to a drawn "element
line" and mark the points of intersecting isolines on the edge
of the paper.
2. Move the edge of the piece of paper around the
isoline drawing in order to find the place where these marks coincid
(intersect) with the isolines. When this happens an equal "element"
has been found.
It is possible to find an almost countless number
of such congruent pair of "element-lines" based upon the
3D geometry described on the previous pages.
|
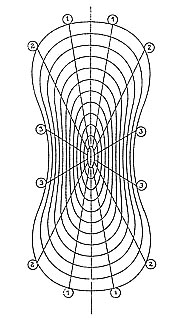
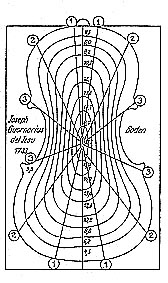
The computer calculated iso line layout for an arching shape
with equal width for "upper" and "lower"parts
This figure has no real violin isoline layout.
It's only shown to illustrate the "element" congruence
more obvious.
The figure shows the iso line layout for a computer calculated
arching shape with equal width for "upper and "lower"
part.
There is complete congruence of shape in each quarter (90 dgre
sectors). The layout is completed with "elements"
(straight lines) marking the place of 3 different cross sections
in each quarter, which are equal in shape (congruent).
|
|
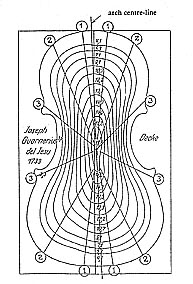
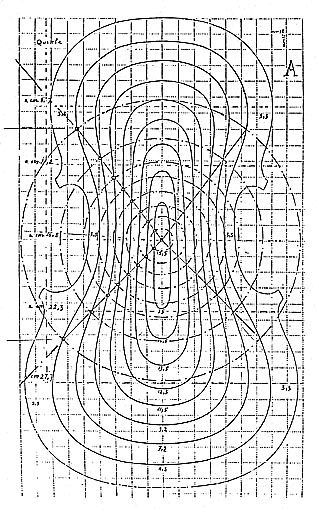
The
computer calculated iso-line layout for a normal violin arching
with different width for "upper" and "lower"
parts
This is a correct violin iso-line model
The figure shows computer calculated "iso
lines" based upon the described 2D and 3D geometry, after
the rotation of the main geometric layouts have taken place.
These iso lines are comparable to the measured
ones by Möckel. (Stradivarius and Guarnmeri del Gesu).
The straight (1...4) equal numbered "elements"
mark the exact places on the arching surface that are congruent.
So the number 2 "elements" in the "upper part
" are congruent to the number 2 in the "lower part"
in spite of a different (wider-smaller) layout of the isolines.
|
|
|
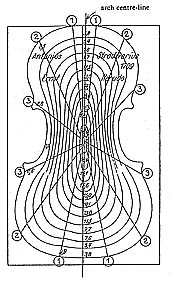
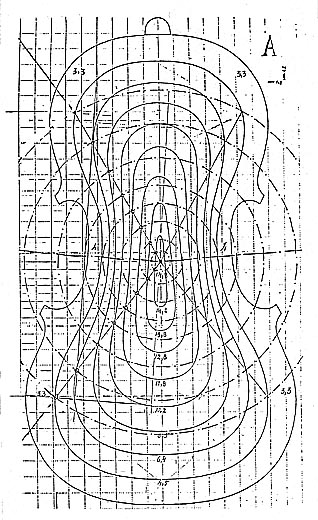
The
Stradivarius iso line layout measured by Otto Möckel
The left figure shows the measured belly in
its state of condition. In spite of the hand made shape it is
easy to find congruent "elements" in and between both
"upper" and "lower" part of the arching,
here marked with equal line numbers.
The right figure shows the measured back in
its state of condition.
|
|
|
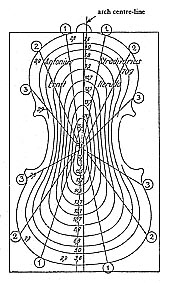
The Guarneri del Gesu iso line
layout measured by Otto Möckel
The left figure shows the measured belly in
its state of condition. In spite of the hand made shape it is
easy to find congruent "elements" in and between both
"upper" and "lower" part of the arching,
here marked with equal line numbers.
The right figure shows the measured back in
its state of condition.
|
|
The
Sacconi iso line layout for the "belly" as an assumption
to createan "average" Stradivarius arching shape
This figure shows Sacconis attemt to construct
a 3D model by 2D geometric layout for a "belly" arching
shape .
It seems obvious that it is a 2D-construction
since all intersection points are positioned on circular arcs
intersecting straight lines.
The figure is divided into 4 sectors marked
by the 4 congruent shaped "elements" on the surface.
Within the waist sector circumscribed by these 4 element lines
there is complete congruence of shape not only comparing left
and right but also up and down.. The dividing angle marksout
the image line of the congruent picture.
It is not possible to find any connection between
the "upper" and "lower" sectors.
The center of the "element" image
is not in the center of the arching shape.
No equal "elements" can be found covering
the "upper" and "lower" parts of the shell.
Only a limited sector in the "waist" has this quality.
|
|
The
Sacconi iso line layout of the "back arching" as an
assumption to renderan "average" Stradivarius arching
shape
This figure shows Sacconis attemt to construct
a 3D model by 2D geometric layouts for a "back" arching
shape of an average Stradivarius violin.
It seems obvious that it is a 2D-construction
since all intersection points are positioned on circular arcs
intersecting straight lines.
The picture is divided into 4 sectors marked
by the 4 congruent shaped "beams" on the surface.
Within the waist sector circumscribed by these 4 line there
is complete congruence of shape not only comparing left and
right but also up and down.. The dividing angle marks out the
image line of the congruent picture.
It is not possible to find any connection between
the "upper" and "lower" sectors.
The center of the "element" image
is not in the center of the arching shape.
No equal "elements" can be found covering
the "upper" and "lower" parts of the shell.
Only a limited sector in the "waist" has this quality.
|